MAPS - Minnesota Automated Plate Scanner Catalog of the POSS I
Home
Galactic Asymmetry
Quick Links

Parameters

Select which parameters you want to examine:

'photom' Table Parameters

The 'photom' database table stores information describing the photometric fits performed (both for 'stellar' and 'integrated' magnitudes) for each POSS I plate in the MAPS Catalog. The following photometric fit parameters are stored for each field in the MAPS Catalog:

Field Name Definition
possfield MAPS POSS I Field Name
possnumber MAPS POSS I Field Number
emul The emulsion of the plate. Either 'O' for the blue-sensitive Kodak 103a-O emulsion and 'E' for the red-sensitive Kodak 103a-E emulsion. The plot below shows the spectral response of these emulsions versus UBVRI filters.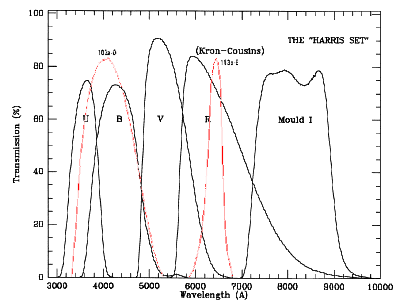
sb0, r0, beta, rm, gamma These are the values of the coefficients used in the fit of the diameter-magnitude relation used to determine the magnitude of a point-like (non-extended) object.

The function fit was a variant of the King and Kormendy form of the PSF functions (King (1971) and Kormendy (1973)) and has the form:

   mag(diam) = SB0 + 2.5 log10[(1+(diam/R0)^2)^BETA + (diam/RM)^GAMMA]
where "diam" is the "areal" diameter in EREs (By "areal" diameter, we mean the diameter determined by taking the surface area of the scanned object in square EREs, and then computing the diameter of a circle with the same area.). The five parameters fit to the data are SB0, BETA, R0, GAMMA, and RM. This fit is accomplished via a non-linear least squares fit and is done independently for the O and E plates.

Nstars Number of stars used in the fit
Nflag Number of stars flagged and not used in the fit
calsrc Photometric calibration sources on the O and E plates, respectively.
  • 0 - only Guide Star Catalog
  • 1 - CCD calibration
  • 2 - Photoelectric measurements
  • 3 - both CCD and Photoelectric measurements
This is the same value as recorded in the 'plates' table for this field and emulsion.
mindia, maxdia The "areal" diameters (in ERE) of the smallest and largest stars used in the fit
rms The RMS of the entire fit for the diameter-magnitude relation. If undefined, its value is set to "99.9000".
rms_08_14 The RMS of fit for the diameter-magnitude relation between 8th and 14th magnitude. If undefined, its value is set to "99.9000".
rms_14_20 The RMS of fit for the diameter-magnitude relation between 14th and 20th magnitude. If undefined, its value is set to "99.9000".
rms_20_22 The RMS of fit for the diameter-magnitude relation between 20th and 22th magnitude. If undefined, its value is set to "99.9000".
D_sky The photographic grain density of the sky determined from a low-resolution background scan of the plate.
D_max, alpha_DI, beta_DI, gamma_DI The density-to-intensity relation used to compute the integrated magnitudes of non-stellar (galactic) images is fit by a function developed by Greg Aldering The density-to-intensity function is assumed to have a form: 
   D(I) = D_MAX*(1 - exp[ALPHA*(I^(BETA*(I^GAMMA)))])
motivated by a physical model for response of photographic grains to incoming photons. Note that in addition to the four parameters fit (ALPHA, BETA, GAMMA, and D_MAX), the intensity I in the above equation is (I_STAR+I_SKY)/I_REF, so I_SKY is another parameter to be fit. As before, the fit is performed independently on the O and E plates. This allows a check of the D-to-I transformation using the fit I_SKY.
I_sky Estimate of the sky intensity based the sky density and the fit of D(I). This sky intensity cooresponds to flux per square ERE on the and so one could convert this to sky surface brightness, mu_sky, in mag/arcsecond^2, can be computed from this intensity using the relation: 
  mu_sky = -2.5*log10(I_sky/(ERE^2/arcsecond^2))
where (ERE^2/arcsecond^2) = (0.0245 ERE/arcsecond)^2.
I_ref Estimate of the reference intensity.
I_thresh Estimate of the threshold intensity.
seeing The seeing of the sky are determined by the PSF of stars used in fitting the density-to-intensity relation.